（本小题满分15分）已知函数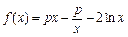
．
（I） 若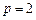
，求曲线
在点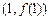
处的切线方程；
若函数在其定义域内为增函数，求正实数
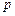的取值范围；
（III）设函数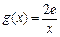
，若在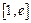
上至少存在一点
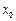，使得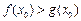
成立，求实数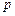的取值范围．
相关试题
<α<π,0<β<
,cos(β－α)= 
,求sinβ的值.
，
，那么
为锐角，且cos
=
,cos
=
，求
的值.
，当
为何值时，
平面
，
平面
，
为
的中点且
∥平面
.
的长；
和平面
所成角的正切值.
相关知识点
推荐套卷
（本小题满分15分）已知函数．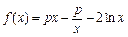
（I） 若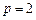，求曲线在点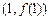处的切线方程；
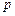若函数在其定义域内为增函数，求正实数的取值范围；
（III）设函数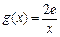，若在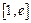上至少存在一点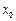，使得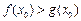成立，求实数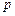的取值范围．
粤公网安备 44130202000953号