(本小题满分12分)已知二次函数f(x)=ax2+bx+c和一次函数g(x)=－bx，其中a、b、c满足a>b>c,a+b+c=0,(a,b,c∈R)
(1)求证：函数
图象交于不同的两点；
(2)设（1）问中交点为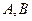
,求线段AB在x轴上的射影A1B1的长的取值范围。
相关试题
．
的单调递增区间；
的方程
在
]上有两个不同的解，求实数
的取值范围．
的各项均为正数，且
，
，求数列
的前
项和．
是单位圆
上的点，点
是单位圆与
轴正半轴的交点，点
在第二象限．记
且
．
的值．相关知识点
推荐套卷
(本小题满分12分)已知二次函数f(x)=ax2+bx+c和一次函数g(x)=－bx，其中a、b、c满足a>b>c,a+b+c=0,(a,b,c∈R)
(1)求证：函数图象交于不同的两点；
(2)设（1）问中交点为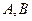,求线段AB在x轴上的射影A1B1的长的取值范围。
粤公网安备 44130202000953号