（本小题满分12分）如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧棱PD
底面ABCD，PD=DC，E是PC的中点，作EFPB交PB于点F
（1）、证明：PA∥平面DEB；
（2）、证明：PB平面EFD；
（3）、设PD=1，求DF的长。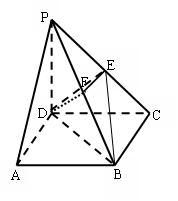
相关试题
经过两点
，
.
的圆心在直线
和
，求圆
与
的交点P，
的直线
的方程;
与直线
垂直,求
.
经过点(0，－2)，其倾斜角是60°．
,离心率
.
与椭圆交于不同的两点
，且线段
的中点的横坐标为
，求直线推荐套卷
（本小题满分12分）如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧棱PD底面ABCD，PD=DC，E是PC的中点，作EFPB交PB于点F
（1）、证明：PA∥平面DEB；
（2）、证明：PB平面EFD；
（3）、设PD=1，求DF的长。
粤公网安备 44130202000953号