（本小题满分12分）
从某批产品中，有放回地抽取产品二次，每次随机抽取1件，假设事件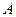
：“取出的2件产品都是二等品”的概率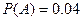
（1）求从该批产品中任取1件是二等品的概率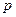
；
（2）若该批产品共10件，从中任意抽取2件，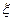
表示取出的2件产品中二等品的件数，求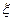的分布列．
，
，且
，
.
，
，
时，求函数
的最大值；
，且
在
的取值范围.
中，
，
，
；
，求证：数列
是等差数列.
，
，
，且
，
时，求
的值；
求
的取值范围.
，
，求
.推荐套卷
（本小题满分12分）
从某批产品中，有放回地抽取产品二次，每次随机抽取1件，假设事件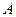：“取出的2件产品都是二等品”的概率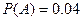
（1）求从该批产品中任取1件是二等品的概率；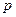
（2）若该批产品共10件，从中任意抽取2件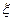，表示取出的2件产品中二等品的件数，求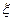的分布列．
粤公网安备 44130202000953号