(本小题满分12分)
哈尔滨冰雪大世界每年冬天都会吸引大批游客,现准备在景区内开设经营热饮等食品的店铺若干。根据以往对500名40岁以下(含40岁)人员和500名40岁以上人员的统计调查,有如下一系列数据:40岁以下(含40岁)人员购买热饮等食品的有260人,不购买热饮食品的有240人;40岁以上人员购买热饮等食品的有220人,不购买热饮等食品的有280人,请根据以上数据作出2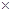 2列联表,并运用独立性检验思想,判断购买热饮等食品与年龄(按上述统计中的年龄分类方式)是否有关系?
2列联表,并运用独立性检验思想,判断购买热饮等食品与年龄(按上述统计中的年龄分类方式)是否有关系?
注:要求达到99.9%的把握才能认定为有关系。
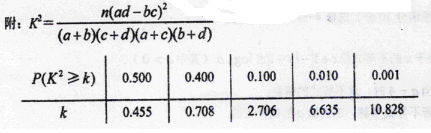 s
s