如图，在直三棱柱ABC—A1B1C1中，AB⊥BC，P为A1C1的中点，AB=BC=kPA。
（I）当k=1时，求证PA⊥B1C；
（II）当k为何值时，直线PA与平面BB1C1C所成的角的正弦值为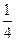
，并求此时二面角A—PC—B的余弦值。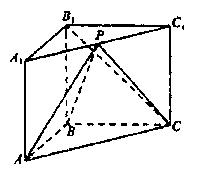
相关试题
，
.
的取值范围，使
在闭区间
上是单调函数；
时，函数
的最大值是关于
.求
，恒有
成立.
．
的值；
的不等式：
在区间
上有解，求实数
的取值范围．
，
.
的值．
的最小正周期。
．
时，求函数
在
上的值域；
，若存在
，使得以
为三边长的三角形不存在，求实数
的取值范围．推荐套卷
如图，在直三棱柱ABC—A1B1C1中，AB⊥BC，P为A1C1的中点，AB=BC=kPA。
（I）当k=1时，求证PA⊥B1C；
（II）当k为何值时，直线PA与平面BB1C1C所成的角的正弦值为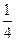，并求此时二面角A—PC—B的余弦值。
粤公网安备 44130202000953号