(本小题满分12分)
某产品生产厂家根据以往的生产销售经验得到下面有关销售的统计规律:每生产产品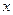 (百台),其总成本为
(百台),其总成本为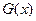 万元,其中固定成本为2万元,并且每生产100台的生产成本为1万元(总成本=固定成本+生产成本),销售收入
万元,其中固定成本为2万元,并且每生产100台的生产成本为1万元(总成本=固定成本+生产成本),销售收入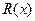 满足
满足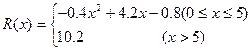 。假定该产品销售平衡,
。假定该产品销售平衡, 那么根据上述统计规律。
那么根据上述统计规律。
(1)要使工厂有盈利,产品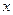 应控制在什么范围?
应控制在什么范围?
(2)工厂生产多少台产品时赢利最大?并求此时每台产品的售价为多少?
推荐套卷
(本小题满分12分)
某产品生产厂家根据以往的生产销售经验得到下面有关销售的统计规律:每生产产品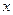 (百台),其总成本为
(百台),其总成本为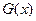 万元,其中固定成本为2万元,并且每生产100台的生产成本为1万元(总成本=固定成本+生产成本),销售收入
万元,其中固定成本为2万元,并且每生产100台的生产成本为1万元(总成本=固定成本+生产成本),销售收入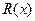 满足
满足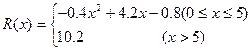 。假定该产品销售平衡,
。假定该产品销售平衡, 那么根据上述统计规律。
那么根据上述统计规律。
(1)要使工厂有盈利,产品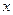 应控制在什么范围?
应控制在什么范围?
(2)工厂生产多少台产品时赢利最大?并求此时每台产品的售价为多少?