已知关于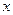
的不等式
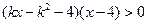，其中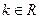
.
⑴当
变化时，试求不等式的解集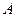
；
⑵对于不等式的解集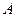，若满足
（其中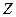
为整数集）. 试探究集合
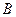能否为有限集？若能，求出使得集合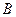中元素个数最少的的所有取值，并用列举法表示集合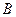；若不能，请说明理由.
相关试题
相关知识点
推荐套卷
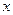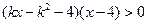已知关于的不等式，其中.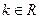
⑴当变化时，试求不等式的解集；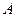
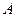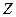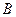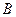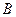⑵对于不等式的解集，若满足（其中为整数集）. 试探究集合能否为有限集？若能，求出使得集合中元素个数最少的的所有取值，并用列举法表示集合；若不能，请说明理由.
粤公网安备 44130202000953号