（本小题12分）已知函数f(x)＝ax3＋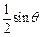
x2－2x＋c，过点
，且在（－2，1）内单调递减，在[1，
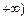上单调递增。
（1）证明sinθ=1，并求f(x)的解析式。
（2）若对于任意的x1，x2∈[m，m＋3]（m≥0），不等式|f(x1)－f(x2)|≤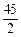
恒成立。试问这样的m是否存在，若存在，请求出m的范围，若不存在，说明理由。
（3）已知数列{an}中，a1∈
，an＋1＝f(an)，求证：an＋1>8·lnan（n∈N*）。
（
＞
＞0）上一点
（3，4），若
，求椭圆方程。
图象上的点
处的切线方程为
。若函数
在
=-2处有极值，求
共焦点，它们的离心率之和为
，求双曲线方程。
方程
有两个不相等的负根，
方程
无实数根，若“
或
”为真，“
的取值范围。
与
互相垂直，其中
．
和
的值；
，求
的值．推荐套卷
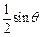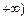（本小题12分）已知函数f(x)＝ax3＋x2－2x＋c，过点，且在（－2，1）内单调递减，在[1，上单调递增。
（1）证明sinθ=1，并求f(x)的解析式。
（2）若对于任意的x1，x2∈[m，m＋3]（m≥0），不等式|f(x1)－f(x2)|≤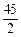恒成立。试问这样的m是否存在，若存在，请求出m的范围，若不存在，说明理由。
（3）已知数列{an}中，a1∈，an＋1＝f(an)，求证：an＋1>8·lnan（n∈N*）。
粤公网安备 44130202000953号