（本小题满分14分）椭圆E的中心在原点O，焦点在x轴上，离心率
，过点C（-1，0）的直线l交椭圆于A、B两点，且满足：
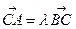（λ≥2）。
（1）若λ为常数，试用直线l的斜率k（k≠0）表示三角形OAB的面积；
（2）若λ为常数，当三角形OAB的面积取得最大值时，求椭圆E的方程；
（3）若λ变化，且λ=k2+1，试问：实数λ和直线l的斜率k（k∈R）分别为何值时，椭圆E的短半轴长取得最大值？并求出此时的椭圆方程。
相关试题
最小正周期和单调增区间
时，求函数
的值域。
满足：（1）
，（2）被
轴截得的弦长为2，（3）在
轴截距为6，求此函数解析式。
≤1的解集
。
的直径
，
为圆周上一点，
，过
，过
作
，垂足为
，求∠DAC
.
时，求函数
的最值；
使
的图象与
无公共点.推荐套卷
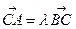（本小题满分14分）椭圆E的中心在原点O，焦点在x轴上，离心率，过点C（-1，0）的直线l交椭圆于A、B两点，且满足：（λ≥2）。
（1）若λ为常数，试用直线l的斜率k（k≠0）表示三角形OAB的面积；
（2）若λ为常数，当三角形OAB的面积取得最大值时，求椭圆E的方程；
（3）若λ变化，且λ=k2+1，试问：实数λ和直线l的斜率k（k∈R）分别为何值时，椭圆E的短半轴长取得最大值？并求出此时的椭圆方程。
粤公网安备 44130202000953号