在立体图形P－ABCD中，底面ABCD是一个直角梯形，∠BAD＝90°，AD∥BC，
AB＝BC＝a，AD=PA＝2a，E是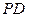
边的中点，且PA⊥底面ABCD。
（1）求证：BE⊥PD
（2）求证：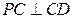
（3）求异面直线AE与CD所成的角．
相关试题
中，平面
平面
，
，
，
。
，
，求四面体
为
，求异面直线
与
所成角的余弦值。
中，底面
是矩形，已知
，
，
，
，
。
平面
；
的正切值的大小。
中，平面
平面
，
，
，
、
分别是
、
的中点。
平面
；
平面
。
推荐套卷
在立体图形P－ABCD中，底面ABCD是一个直角梯形，∠BAD＝90°，AD∥BC，
AB＝BC＝a，AD=PA＝2a，E是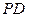边的中点，且PA⊥底面ABCD。
（1）求证：BE⊥PD
（2）求证：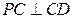
（3）求异面直线AE与CD所成的角．
粤公网安备 44130202000953号