（本小题共12分）设x=3是函数f (x) = (x2+ax+b)·e3-x (x∈R)的一个极值点。
⑴求a与b的关系式，(用a表示b)，并求f(x)的单调区间。
⑵设a>0，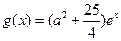 
，若存在ε1，ε2∈[0，4]，使｜f (ε1)-g (ε2)｜<1成立，求a的取值范围。
上，且到
轴的距离恰等于圆的半径，在
轴上截得的弦长为
，求此圆的方程．
的底边长分别为6和4，高为3，求这个等腰梯形的外接圆的方程，并求这个圆的圆心坐标和半径长．
内一点
，过点
的直线
的倾斜角为
，直线
，
．（1）当
时，求
的长；（2）当弦
被圆
截得的弦
的长．
的圆经过点
和
，且圆心
上，求圆心为推荐套卷
（本小题共12分）设x=3是函数f (x) = (x2+ax+b)·e3-x (x∈R)的一个极值点。
⑴求a与b的关系式，(用a表示b)，并求f(x)的单调区间。
⑵设a>0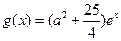， ，若存在ε1，ε2∈[0，4]，使｜f (ε1)-g (ε2)｜<1成立，求a的取值范围。
粤公网安备 44130202000953号