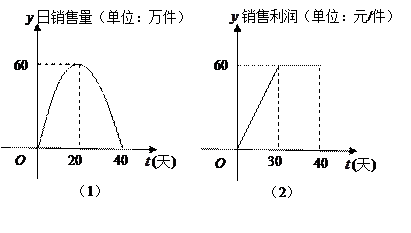(本小题满分12分)
某公司是专门生产健身产品的企业，第一批产品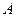
上市销售40天内全部售完，该公司对第一批产品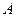上市后的市场销售进行调研，结果如图（1）、（2）所示．其中（1）的抛物线表示的是市场的日销售量与上市时间的关系；（2）的折线表示的是每件产品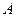的销售利润与上市时间的关系．
（1）写出市场的日销售量
与第一批产品A上市时间t的关系式；
（2）第一批产品A上市后的第几天，这家公司日销售利润最大，最大利润是多少？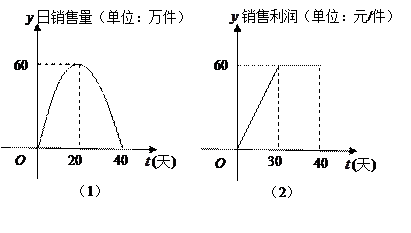
,
，且
的取值范围；
，试求
的取小值，并求此时
的值。
．求
的最大值及最小正周期.
R
.
的最小正周期;
的值．
，
， 
⊥
, 且－＜
＜． 求
|
的最大值和最小值．推荐套卷
(本小题满分12分)
某公司是专门生产健身产品的企业，第一批产品上市销售40天内全部售完，该公司对第一批产品上市后的市场销售进行调研，结果如图（1）、（2）所示．其中（1）的抛物线表示的是市场的日销售量与上市时间的关系；（2）的折线表示的是每件产品的销售利润与上市时间的关系．
（1）写出市场的日销售量与第一批产品A上市时间t的关系式；
（2）第一批产品A上市后的第几天，这家公司日销售利润最大，最大利润是多少？
粤公网安备 44130202000953号