如图，△ABC内接于圆O,AB是圆O的直径，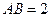
，
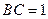，设AE与平面ABC所成的角为
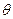,且
,
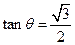四边形DCBE为平行四边形，DC
平面ABC．
（1）求三棱锥C－ABE的体积；
（2）证明：平面ACD平面ADE；
（3）在CD上是否存在一点M，使得MO//平面ADE？证明你的结论．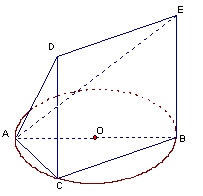
相关试题
的前
项和为
,
．
,求
；
,求
的前6项和
．
. 
的值．
的解集为
．
；
．
．
的最大值．
的前
项和为
，常数
，且
对一切正整数
，
，求证： 
<4推荐套卷
如图，△ABC内接于圆O,AB是圆O的直径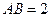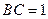，，，设AE与平面ABC所成的角为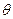,且,
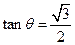四边形DCBE为平行四边形，DC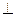平面ABC．
（1）求三棱锥C－ABE的体积；
（2）证明：平面ACD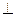平面ADE；
（3）在CD上是否存在一点M，使得MO//平面ADE？证明你的结论．
粤公网安备 44130202000953号