2009年,福特与浙江吉利就福特旗下的沃尔沃品牌业务的出售在商业条款上达成一致,据专家分析,浙江吉利必须完全考虑以下四个方面的挑战:第一个方面是企业管理,第二个方面是汽车制造技术,第三个方面是汽车销售,第四个方面是人才培养.假设以上各种挑战各自独立,并且只要第四项不合格,或第四项合格且前三项中至少有两项不合格,企业将破产,若第四项挑战失败的概率为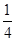 ,其他三项挑战失败的概率分别为
,其他三项挑战失败的概率分别为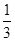 .
.
(1)求浙江吉利不破产的概率;
(2)专家预测:若四项挑战均成功,企业盈利15亿美元;若第一、第二、第三项挑战中仅有一项不成功且第四项挑战成功,企业盈利5亿美元;若企业破产,企业将损失10亿美元.设浙江吉利并购后盈亏为X亿美元,求随机变量X的期望.