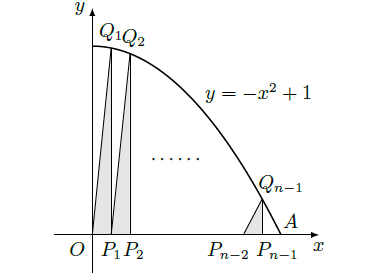
如图,抛物线
与
轴的正半轴交于点
,将线段
的
等分点从左至右依次记为
,过这些分点分别作
轴的垂线,与抛物线的交点依次为
,从而得到
个直角三角形
,当
时,这些三角形的面积之和的极限为 .
相关知识点
推荐套卷
如图,抛物线
与
轴的正半轴交于点
,将线段
的
等分点从左至右依次记为
,过这些分点分别作
轴的垂线,与抛物线的交点依次为
,从而得到
个直角三角形
,当
时,这些三角形的面积之和的极限为 .
