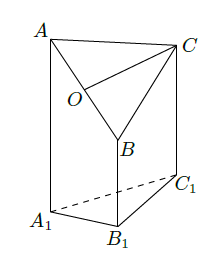
如图是一个直三棱柱（以A1B1C为底面）被一平面所截得到的几

更新 2022-09-03
科目数学
题型解答题
难度较难
浏览 1404

如图是一个直三棱柱（以 $A_{1} B_{1} C$ 为底面）被一平面所截得到的几何体，截面为 $A B C$ ．已知 $A_{1} B_{1} = B_{1} C_{1} = 1, ∠ A_{1} B_{1} C_{1} = 90^{o}, A A_{1} = 4, B B_{1} = 2, C C_{1} = 3$ ， $∠ A_{l} B_{l} C_{1} ＝ 90 °$ ，
$A A_{l} ＝ 4$ ， $B B_{l} ＝ 2$ ， $C C_{l} ＝ 3$ ．
（1）设点 $O$ 是 $A B$ 的中点，证明： $O C ∥$ 平面 $A_{1} B_{1} C_{1}$

（2）求二面角 $B - A C - A_{1}$ 的大小；
（3）求此几何体的体积．

登录免费查看答案和解析

相关试题

某电视生产企业有A、B两种型号的电视机参加家电下乡活动，若企业投放A、B两种型号电视机的价值分别为a、b万元，则农民购买电视机获得的补贴分别为万元（m＞0且为常数）．已知该企业投放总价值为10万元的A、B两种型号的电视机，且A、B两种型号的投放金额都不低于1万元．
（1）请你选择自变量，将这次活动中农民得到的总补贴表示为它的函数，并求其定义域；
（2）求当投放B型电视机的金额为多少万元时，农民得到的总补贴最大？

题型：未知
难度：未知

收藏答案/解析

如图，在等腰梯形ABCD中，AB∥DC，AB = 4，CD = 2，等腰梯形的高为3，O为AB中点，PO⊥平面ABCD，垂足为O，PO = 2，EA∥PO．

（1）求证：BD⊥平面EAC；
（2）求二面角E—AC—P的平面角的余弦值．

题型：未知
难度：未知

收藏答案/解析

“上海世博会”将于2010年5月1日至10月31日在上海举行。世博会“中国馆·贵宾厅”作为接待中外贵宾的重要场所，其中陈列的艺术品是体现兼容并蓄、海纳百川的重要文化载体，为此，上海世博会事物协调局将举办“中国2010年上海世博会‘中国馆·贵宾厅’艺术品方案征集”活动．某地美术馆从馆藏的中国画、书法、油画、陶艺作品中各选一件代表作参与应征，假设这四件代表作中中国画、书法、油画入选“中国馆·贵宾厅”的概率均为，陶艺入选“中国馆·贵宾厅”的概率为．假定这四件作品是否入选相互没有影响．
（1）求该地美术馆选送的四件代表作中恰有一件作品入选“中国馆·贵宾厅”的概率;
（2）设该地美术馆选送的四件代表作中入选“中国馆·贵宾厅”的作品件数为随机变量，求的数学期望.