(1) 以直角坐标系的原点 为极点,
为极点, 轴的正
轴的正 半轴为极
半轴为极 轴。已知点
轴。已知点 的直角坐标为(1,-5),点
的直角坐标为(1,-5),点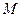 的极坐标为
的极坐标为 若直线
若直线 过点
过点 ,且倾斜角为
,且倾斜角为 ,圆
,圆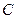 以
以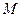 为圆心、
为圆心、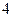 为半径。(I)求直线
为半径。(I)求直线 的参数方程和圆
的参数方程和圆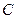 的极坐标方程;(II)试判定直线
的极坐标方程;(II)试判定直线 和圆
和圆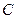 的位置关系.
的位置关系.
(2)把曲线 先进行横坐标缩为原来的一半,纵坐标保持不变的伸缩变换,再做关于
先进行横坐标缩为原来的一半,纵坐标保持不变的伸缩变换,再做关于 轴的反射变换变为曲线
轴的反射变换变为曲线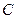 ,求曲线
,求曲线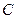 的方程.
的方程.
(3)关于 的一元二次方程
的一元二次方程 对任意
对任意 无实根,求实数
无实根,求实数 的取值范围.
的取值范围.
相关知识点
推荐套卷
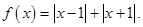
 的解集;
的解集;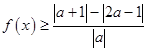 对任意实数
对任意实数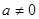 恒成立,求实数x的取值范围.
恒成立,求实数x的取值范围. 的前
的前 项和记为
项和记为 ,点
,点 在直线
在直线 ,
, .
. 为何值时,数列
为何值时,数列 是数列
是数列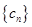 的前
的前
 的两焦点分别为
的两焦点分别为 ,长轴长为6.
,长轴长为6. 的标准方程;
的标准方程; 且斜率为1的直线交椭圆
且斜率为1的直线交椭圆 两点,求线段
两点,求线段 的长度.
的长度. .
. 在区间
在区间 上的最大值;
上的最大值; 在区间
在区间 上单调递增,试求m的取值范围.
上单调递增,试求m的取值范围. 分别是
分别是 中角
中角 的对边,且
的对边,且
 的大小;
的大小; 求
求 的值.
的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号