已知函数f(x)是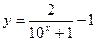
（x
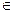R）的反函数，函数g(x)的图象与函数
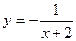的图象关于直线x=－2成轴对称图形，设F(x)=f(x)+g(x).
（1）求函数F(x)的解析式及定义域；
（2）试问在函数F(x)的图象上是否存在两个不同的点A,B，使直线AB恰好与y轴垂直？若存在，求出A,B坐标；若不存在，说明理由.
．
时，写出
的单调区间；
时，求
的方程
的解的个数．
的不等式：
．
是定义在
上的增函数．
，试比较
的大小，并说明理由；
，不等式
恒成立，求实数
的取值范围．
的定义域为集合A，函数
的定义域为集合B．
，求实数
的取值范围．
．
的值；
的值域．推荐套卷
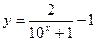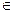已知函数f(x)是 （xR）的反函数，函数g(x)的图象与函数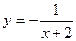的图象关于直线x=－2成轴对称图形，设F(x)=f(x)+g(x).
（1）求函数F(x)的解析式及定义域；
（2）试问在函数F(x)的图象上是否存在两个不同的点A,B，使直线AB恰好与y轴垂直？若存在，求出A,B坐标；若不存在，说明理由.
粤公网安备 44130202000953号