（本小题满分15分）
如图，我市现有自市中心
通往正西和东偏北
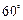方向的两条公路．为了解决市区交通拥挤问题，市政府决定修建一条环城公路，分别在通往正西和东偏北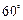方向的两条公路上选取
两点，环城公路为间的直线段，设计要求市中心到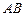
段的距离为10km，且间的距离最小，请你确定两点的位置
 |
相关试题
，
，且
，求
的值．
，若
的最大值为0，最小值为－4，试求
与
的值，并求
的最大、最小值及相应的
值．
; 
的值；
，
的最小值为
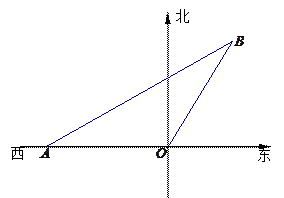，求实数m的值.推荐套卷
（本小题满分15分）
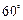如图，我市现有自市中心通往正西和东偏北方向的两条公路．为了解决市区交通拥挤问题，市政府决定修建一条环城公路，分别在通往正西和东偏北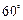方向的两条公路上选取两点，环城公路为间的直线段，设计要求市中心到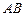段的距离为10km，且间的距离最小，请你确定两点的位置
|
粤公网安备 44130202000953号