（理）已知直线
的参数方程为
（t为参数），曲线C的参数方程为
（
为参数），直线与曲线C相交于
两点，又点
的坐标为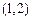
．
求：（1）线段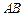
的中点坐标；
（2）线段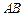的长；
（3）
的值．
（文）已知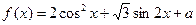
（
，
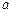为常数）．
（1）若
，求
的最小正周期；
（2）若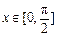
时，的最大值为4，求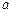的值．
相关试题
：函数
的图象与
轴没有公共点，命题
，若命题
为真命题，求实数
的取值范围
R
, 
.
的单调区间；
的方程
为自然对数的底数)只有一个实数根, 求
的值.
为等差数列，且
，
．
，求证：数列
是等比数列；
，求数列
的前
项和
.
中，
、
分别为
、
的中点．
//平面
；
；
的体积．
相关知识点
推荐套卷
（理）已知直线的参数方程为（t为参数），曲线C的参数方程为（为参数），直线与曲线C相交于两点，又点的坐标为．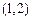
求：（1）线段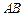的中点坐标；
（2）线段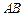的长；
（3）的值．
（文）已知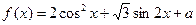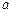（，为常数）．
（1）若，求的最小正周期；
（2）若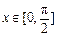时，的最大值为4，求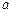的值．
粤公网安备 44130202000953号