(本小题满分10分)
从甲、乙两名学生中选拔一人参加射箭比赛,为此需要对他们的射箭水平进行测试.现这两名学生在相同条件下各射箭7次,命中的环数如下:
| 甲 |
10 |
8 |
6 |
9 |
7 |
6 |
10 |
| 乙 |
10 |
9 |
8 |
6 |
7 |
8 |
8 |
(1)计算甲、乙两人射箭命中环数的平均数和方差;
(2)比较两个人的成绩,然后决定选择哪名学生参加射箭比赛.
相关知识点
推荐套卷
 .
.


 的值,
的值,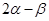 的值.
的值. 轴所得弦长为
轴所得弦长为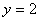 ;②被
;②被 轴分成两段圆弧,其弧长的比为
轴分成两段圆弧,其弧长的比为 ;③圆心到直线
;③圆心到直线 :
: 的距离为
的距离为 的圆的方程。
的圆的方程。 粤公网安备 44130202000953号
粤公网安备 44130202000953号