设椭圆M：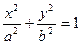
(a＞b＞0)的离心率为
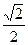，长轴长为
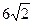，设过右焦点F倾斜角
为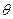
的直线交椭圆M于A，B两点。
（Ⅰ）求椭圆M的方程；
（Ⅱ）求证| AB | =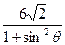
；
（Ⅲ）设过右焦点F且与直线AB垂直的直线交椭圆M于C，
D，求|AB| + |CD|的最小值。
相关试题
的前
项和为
，已知
，求数列
的前
)．(1)判断函数f(x)的奇偶性；
的内角
的对边分别为
，
，
，求
.
.
的值； 
的值.
sinxcosx－1（x∈R）推荐套卷
设椭圆M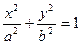：(a＞b＞0)的离心率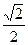为，长轴长为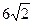，设过右焦点F倾斜角
为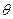的直线交椭圆M于A，B两点。
（Ⅰ）求椭圆M的方程；
（Ⅱ）求证| AB | =；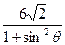
（Ⅲ）设过右焦点F且与直线AB垂直的直线交椭圆M于C，D，求|AB| + |CD|的最小值。
粤公网安备 44130202000953号