设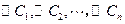 
是圆心在抛物线 
上的一系列圆，它们的圆心的横坐标分别记为 
，已知 
，又 
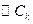
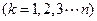都与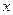 
轴相切，且顺次逐个相邻外切.
（1）求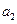 
；
（2）求由 构成的数列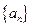 
的通项公式；
（3）求证：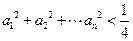 
.
相关试题
矩形ABCD所在平面，PA=AD=
，E为线段PD上一点，G为线段PC的中点.
时，求证：BG//平面AEC.
的最小值及此时x的取值集合；
个单位后所得图象关于y轴对称，求m的最小值。
在
处取得极值。
和
是函数
的极大值还是极小值；
作曲线
的切线，求此切线方程。
在
处取得极值。
和
是函数
的极大值还是极小值；
作曲线
的切线，求此切线方程。
推荐套卷
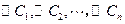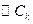
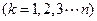设 是圆心在抛物线 上的一系列圆，它们的圆心的横坐标分别记为 ，已知 ，又 都与 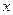轴相切，且顺次逐个相邻外切.
（1）求 ；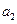
（2）求由 构成的数列 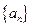的通项公式；
（3）求证： .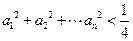
粤公网安备 44130202000953号