（本小题满分12分）
设f(x)是定义在[-1,1]上的奇函数，对于任意的
当
时，都
有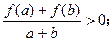
（1）若函数g(x)=f(x-c)和h(x)=f(x-c2)的定义域的交集是空集，求c的取值范围；
（2）判断函数f(x)在[-1,1]上的单调性，并用定义证明。
相关试题
是格点三角形。
点逆时针旋转90o后的图形
；
所经过的路线的长。
，其中
。
÷
中，
，
中，
,
. 连接
、
点
、、
分别为
、
、
、
、
三点在同一直线上，且
，则
的形状是__________，此时
________；
，证明
，并计算
的值（用含
的式子表示）；
的最大值.推荐套卷
（本小题满分12分）
设f(x)是定义在[-1,1]上的奇函数，对于任意的 当时，都
有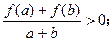
（1）若函数g(x)=f(x-c)和h(x)=f(x-c2)的定义域的交集是空集，求c的取值范围；
（2）判断函数f(x)在[-1,1]上的单调性，并用定义证明。
粤公网安备 44130202000953号