(本题满分10分) 如下的三个图中,左面的是一个长方体截去一个角所得多面体的直观图,它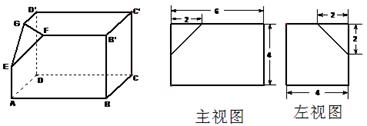
的主视图和左视图在右面画出(单位:cm).
(1)按照给出的尺寸,求该多面体的体积;
(2)在所给直观图中连结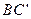 ,证明:
,证明: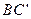 ∥面EFG。
∥面EFG。
推荐套卷
(本题满分10分) 如下的三个图中,左面的是一个长方体截去一个角所得多面体的直观图,它
的主视图和左视图在右面画出(单位:cm).
(1)按照给出的尺寸,求该多面体的体积;
(2)在所给直观图中连结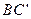 ,证明:
,证明: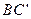 ∥面EFG。
∥面EFG。