(本小题满分14分)一个口袋中装有 个红球
个红球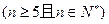 和5个白球,一次摸奖从中摸两球,两个球颜色不同则为中奖。
和5个白球,一次摸奖从中摸两球,两个球颜色不同则为中奖。
(1)试用 表示一次摸奖中奖的概率
表示一次摸奖中奖的概率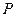 ;
;
(2)若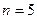 ,求三次摸奖(每次摸奖后放回)恰有一次中奖的概率;
,求三次摸奖(每次摸奖后放回)恰有一次中奖的概率;
(3)记三次摸奖(每次摸奖后放回)恰有一次中奖的概率为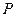 ,当
,当 取多少时,
取多少时,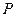 最大?
最大?
推荐套卷
(本小题满分14分)一个口袋中装有 个红球
个红球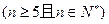 和5个白球,一次摸奖从中摸两球,两个球颜色不同则为中奖。
和5个白球,一次摸奖从中摸两球,两个球颜色不同则为中奖。
(1)试用 表示一次摸奖中奖的概率
表示一次摸奖中奖的概率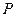 ;
;
(2)若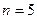 ,求三次摸奖(每次摸奖后放回)恰有一次中奖的概率;
,求三次摸奖(每次摸奖后放回)恰有一次中奖的概率;
(3)记三次摸奖(每次摸奖后放回)恰有一次中奖的概率为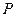 ,当
,当 取多少时,
取多少时,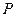 最大?
最大?