已知函数f(x)＝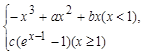
在x＝0，x＝
处存在极值。
（Ⅰ）求实数a,b的值；
（Ⅱ）函数y＝f(x)的图象上存在两点A,B使得△AOB是以坐标原点O为直角顶点的直角三角形，且斜边AB的中点在y轴上，求实数c的取值范围；
(Ⅲ）当c＝e时，讨论关于x的方程f(x)＝kx(k∈R)的实根个数。
相关试题
逆时针方向转90°到QH，
的最值
，定点F（10，4），对于x轴上移动的点P（t，0）作一折线FPQ，使
，若折线FPQ的PQ部分与正方形ABCD的边界有公共点，推荐套卷
已知函数f(x)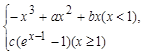＝在x＝0，x＝处存在极值。
（Ⅰ）求实数a,b的值；
（Ⅱ）函数y＝f(x)的图象上存在两点A,B使得△AOB是以坐标原点O为直角顶点的直角三角形，且斜边AB的中点在y轴上，求实数c的取值范围；
(Ⅲ）当c＝e时，讨论关于x的方程f(x)＝kx(k∈R)的实根个数。
粤公网安备 44130202000953号