(本小题满分14分)如图,已知四棱锥P-ABCD中,PA⊥平面CDAB, ABCD是直角梯形,AD∥BC,∠BAD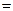 90º,BC
90º,BC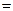 2,PA
2,PA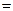 AB
AB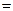 1.
1.
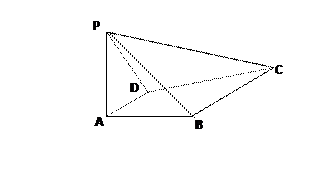
(1)求证:PD⊥AB;
(2)在线段PB上找一点E,使AE//平面PCD;
(3)求点D到平面PBC的距离.
推荐套卷
(本小题满分14分)如图,已知四棱锥P-ABCD中,PA⊥平面CDAB, ABCD是直角梯形,AD∥BC,∠BAD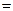 90º,BC
90º,BC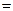 2,PA
2,PA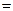 AB
AB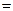 1.
1.
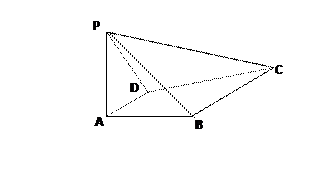
(1)求证:PD⊥AB;
(2)在线段PB上找一点E,使AE//平面PCD;
(3)求点D到平面PBC的距离.