设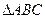 的外心为O,以线段OA、OB为邻边作平行四边形,第四个顶点为D,再以OC、OD为邻边作平行四边形,它的第四个顶点为H 。
的外心为O,以线段OA、OB为邻边作平行四边形,第四个顶点为D,再以OC、OD为邻边作平行四边形,它的第四个顶点为H 。
(1)若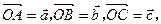 用
用 ;
;
(2)求证: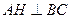 ;
;
(3)设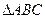 中,
中, 外接圆半径为R, 用
外接圆半径为R, 用
R表示 .(外心是三角形外接圆的圆心)
.(外心是三角形外接圆的圆心)
推荐套卷
设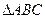 的外心为O,以线段OA、OB为邻边作平行四边形,第四个顶点为D,再以OC、OD为邻边作平行四边形,它的第四个顶点为H 。
的外心为O,以线段OA、OB为邻边作平行四边形,第四个顶点为D,再以OC、OD为邻边作平行四边形,它的第四个顶点为H 。
(1)若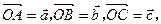 用
用 ;
;
(2)求证: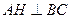 ;
;
(3)设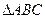 中,
中, 外接圆半径为R, 用
外接圆半径为R, 用
R表示 .(外心是三角形外接圆的圆心)
.(外心是三角形外接圆的圆心)