20． (本小题满分13分)
已知数列{an}有a1 = a，a2 = p（常数p > 0），对任意的正整数n，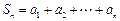
，且
．
(1)求a的值；
(2)试确定数列{an}是否是等差数列，若是，求出其通项公式；若不是，说明理由；
(3)对于数列{bn}，假如存在一个常数b，使得对任意的正整数n都有bn< b，且
，则称b为数列{bn}的“上渐近值”，令
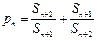，求数列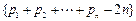
的“上渐近值”．
相关试题
是定义在
上的奇函数，且
，当
时，有
成立．
对所有的
恒成立，求实数m的取值范围．
是定义在R上的偶函数，且
时，
．
的取值范围．
，
．
；
，
满足
试求此时
的最小值．
的定义域是[0,3]，设
的解析式及定义域；
．
的最小正周期及单调递增区间；
，求函数的值域．推荐套卷
20． (本小题满分13分)
已知数列{an}有a1 = a，a2 = p（常数p > 0），对任意的正整数n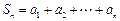，，且．
(1)求a的值；
(2)试确定数列{an}是否是等差数列，若是，求出其通项公式；若不是，说明理由；
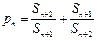(3)对于数列{bn}，假如存在一个常数b，使得对任意的正整数n都有bn< b，且，则称b为数列{bn}的“上渐近值”，令，求数列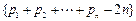的“上渐近值”．
粤公网安备 44130202000953号