（本小题满分10分）
四棱锥P－ABCD中，底面ABCD是正方形，
边长为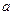
，PD=，PD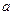⊥平面ABCD
（1）求证: AC⊥PB ；
（2）求二面角A－PB－D的大小；
（3）求四棱锥外接球的半径．
（4）在这个四棱锥中放入一个球，求球的最大半径；
，若
，
，
，试写出满足条件的A、B集合.
，
，
，求实数a的值.
，
，
.
=
，求a的值；
=
，则
.
，则在A中还有两个元素是什么；
.
定义在R上，对任意实数m、n，恒有
且当
推荐套卷
（本小题满分10分）
四棱锥P－ABCD中，底面ABCD是正方形，
边长为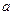，PD=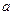，PD⊥平面ABCD
（1）求证: AC⊥PB ；
（2）求二面角A－PB－D的大小；
（3）求四棱锥外接球的半径．
（4）在这个四棱锥中放入一个球，求球的最大半径；
粤公网安备 44130202000953号