(本小题满分13分)
已知定义在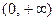 上的三个函数
上的三个函数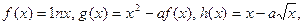 且
且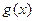 在
在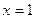 处取得极值.
处取得极值.
(Ⅰ)求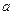 的值及函数
的值及函数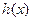 的单调区间;
的单调区间;
(Ⅱ)求证:当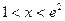 时,恒有
时,恒有 成立;
成立;
(Ⅲ)把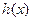 对应的曲线
对应的曲线 按向量
按向量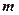
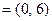 平移后得到曲线
平移后得到曲线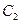 ,求
,求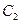 与
与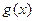 对应曲线
对应曲线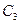 的交点个数,并说明理由.
的交点个数,并说明理由.
推荐套卷
(本小题满分13分)
已知定义在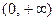 上的三个函数
上的三个函数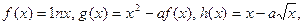 且
且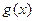 在
在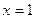 处取得极值.
处取得极值.
(Ⅰ)求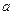 的值及函数
的值及函数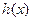 的单调区间;
的单调区间;
(Ⅱ)求证:当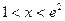 时,恒有
时,恒有 成立;
成立;
(Ⅲ)把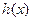 对应的曲线
对应的曲线 按向量
按向量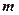
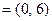 平移后得到曲线
平移后得到曲线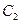 ,求
,求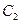 与
与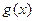 对应曲线
对应曲线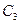 的交点个数,并说明理由.
的交点个数,并说明理由.