(本小题满分12分)
一个袋子内装有若干个黑球,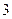 个白球,
个白球,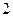 个红球(所有的球除颜色外其它均相同),从中任取
个红球(所有的球除颜色外其它均相同),从中任取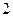 个球,每取得一个黑球得
个球,每取得一个黑球得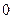 分,每取一个白球得
分,每取一个白球得 分,每取一个红球得
分,每取一个红球得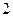 分,已知得
分,已知得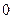 分的概率为
分的概率为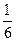 ,用随机变量X表示取
,用随机变量X表示取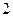 个球的总得分.
个球的总得分.
(Ⅰ)求袋子内黑球的个数;
(Ⅱ)求X的分布列.
相关知识点
推荐套卷
(本小题满分12分)
一个袋子内装有若干个黑球,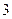 个白球,
个白球,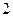 个红球(所有的球除颜色外其它均相同),从中任取
个红球(所有的球除颜色外其它均相同),从中任取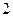 个球,每取得一个黑球得
个球,每取得一个黑球得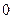 分,每取一个白球得
分,每取一个白球得 分,每取一个红球得
分,每取一个红球得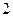 分,已知得
分,已知得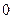 分的概率为
分的概率为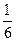 ,用随机变量X表示取
,用随机变量X表示取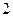 个球的总得分.
个球的总得分.
(Ⅰ)求袋子内黑球的个数;
(Ⅱ)求X的分布列.