某兴趣小组测量电视塔 的高度 (单位 ），如示意图，垂直放置的标杆 高度 ，仰角 .
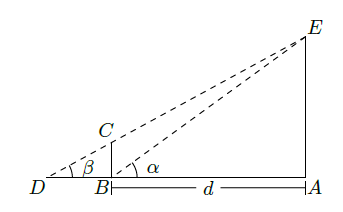
（1）该小组已经测得一组
的值，
,请据此算出H的值
（2）该小组分析若干测得的数据后，发现适当调整标杆到电视塔的距离
（单位
），使
与
之差较大，可以提高测量精确度，若电视塔实际高度为125
，问
为多少时，
最大.
相关试题
，x∈R(其中A＞0，ω＞0,
)的周期为π，且图象上一个最低点为M
.
时，求f(x)的最大值．
，
.
值； (2)求
的值.
.
中，
，前
项的和是
，且
，
.
.推荐套卷
某兴趣小组测量电视塔 的高度 (单位 ），如示意图，垂直放置的标杆 高度 ，仰角 .
（1）该小组已经测得一组
的值，
,请据此算出H的值
（2）该小组分析若干测得的数据后，发现适当调整标杆到电视塔的距离
（单位
），使
与
之差较大，可以提高测量精确度，若电视塔实际高度为125
，问
为多少时，
最大.
粤公网安备 44130202000953号