(本小题满分15分)
已知A、B、C是直线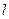
上的不同的三点，O是直线外一点，向量
、
、
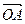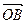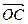满足
，记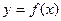
．
（1）求函数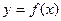的解析式；
（2）若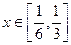
，
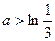,证明：不等式
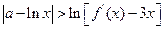成立；
（3）若关于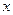
的方程
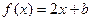在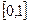
上恰有两个不同的实根，求实数
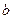的取值范围．
为R上的单调递增函数
(2)
。
的零点；推荐套卷
(本小题满分15分)
已知A、B、C是直线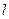上的不同的三点，O是直线外一点，向量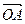、、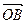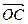满足，记．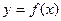
（1）求函数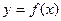的解析式；
（2）若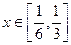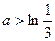，,证明：不等式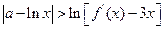成立；
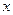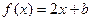（3）若关于的方程在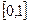上恰有两个不同的实根，求实数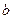的取值范围．
粤公网安备 44130202000953号