如图，四棱锥P-ABCD的底面是平行四边形，PA⊥平面ABCD,
,
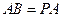,点E是PD上的点，且DE＝
PE(0<
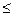1)． 
（Ⅰ） 求证：PB⊥AC；
（Ⅱ） 求的值，使
平面ACE；
（Ⅲ） 当
时，求二面角E-AC-B的大小．
相关试题
上随机取两个数m、n，求关于x的一元二次方程
有实根的概率．袋中有12个小球，其中有外形，重量一样的红球、黑球、黄球、绿球．从中任取一球得到红球的概率是
，得到黑球或黄球的概率是
，得到黄球或绿球的概率也是，分别试求得到黑球、黄球、绿球的概率各是多少？
内任取一个元素，能使代数式
的概率是多少？推荐套卷
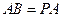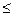如图，四棱锥P-ABCD的底面是平行四边形，PA⊥平面ABCD,,,点E是PD上的点，且DE＝PE(0<1)．
（Ⅰ） 求证：PB⊥AC；
（Ⅱ） 求的值，使平面ACE；
（Ⅲ） 当时，求二面角E-AC-B的大小．
袋中有12个小球，其中有外形，重量一样的红球、黑球、黄球、绿球．从中任取一球得到红球的概率是，得到黑球或黄球的概率是，得到黄球或绿球的概率也是，分别试求得到黑球、黄球、绿球的概率各是多少？
粤公网安备 44130202000953号