(本小题满分12分)已知曲线C的极坐标方程是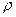 =1,以极点为原点,极轴为
=1,以极点为原点,极轴为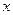 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线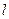 的参数方程为
的参数方程为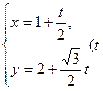 为参数)。
为参数)。
(1)写出直线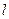 与曲线C的直角坐标方程;
与曲线C的直角坐标方程;
(2)设曲线C经过伸缩变换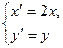 得到曲线
得到曲线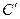 ,设曲线
,设曲线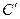 上任一点为
上任一点为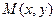 ,求
,求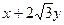 的最小值。
的最小值。
相关知识点
推荐套卷
(本小题满分12分)已知曲线C的极坐标方程是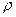 =1,以极点为原点,极轴为
=1,以极点为原点,极轴为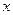 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线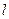 的参数方程为
的参数方程为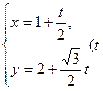 为参数)。
为参数)。
(1)写出直线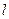 与曲线C的直角坐标方程;
与曲线C的直角坐标方程;
(2)设曲线C经过伸缩变换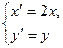 得到曲线
得到曲线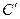 ,设曲线
,设曲线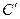 上任一点为
上任一点为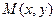 ,求
,求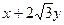 的最小值。
的最小值。