(本小题满分13分)
甲、乙两人各射击一次,击中目标的概率分别是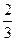 和
和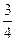 ,假设两个射击是否击中目标,相互之间没有影响;每人各次射击是否中目标相互之间也没有影响。
,假设两个射击是否击中目标,相互之间没有影响;每人各次射击是否中目标相互之间也没有影响。
(1)求甲射击4次,至少有1次未击中目标的概率;
(2)求两人各射击4次,甲恰好击中目标2次且乙恰好击中目标3次的概率;
(3)假设某人连续2次未击中目标,则中止其射击。则乙恰好射击5次后被中止射击的概率是多少?
推荐套卷
(本小题满分13分)
甲、乙两人各射击一次,击中目标的概率分别是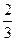 和
和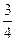 ,假设两个射击是否击中目标,相互之间没有影响;每人各次射击是否中目标相互之间也没有影响。
,假设两个射击是否击中目标,相互之间没有影响;每人各次射击是否中目标相互之间也没有影响。
(1)求甲射击4次,至少有1次未击中目标的概率;
(2)求两人各射击4次,甲恰好击中目标2次且乙恰好击中目标3次的概率;
(3)假设某人连续2次未击中目标,则中止其射击。则乙恰好射击5次后被中止射击的概率是多少?