(本题 12分).过点A(-4,0)向椭圆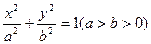 引两条切线,切点分别为B,C,且
引两条切线,切点分别为B,C,且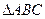 为正三角形.
为正三角形.
(Ⅰ)求 最大时椭圆的方程;
最大时椭圆的方程;
(Ⅱ)对(Ⅰ)中的椭圆,若其左焦点为 ,过
,过 的直线
的直线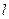 与
与 轴交于点
轴交于点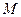 ,与椭圆的一个交点为
,与椭圆的一个交点为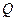 ,且
,且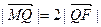 求直线
求直线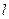 的方程
的方程
推荐套卷
(本题 12分).过点A(-4,0)向椭圆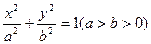 引两条切线,切点分别为B,C,且
引两条切线,切点分别为B,C,且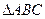 为正三角形.
为正三角形.
(Ⅰ)求 最大时椭圆的方程;
最大时椭圆的方程;
(Ⅱ)对(Ⅰ)中的椭圆,若其左焦点为 ,过
,过 的直线
的直线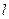 与
与 轴交于点
轴交于点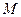 ,与椭圆的一个交点为
,与椭圆的一个交点为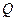 ,且
,且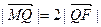 求直线
求直线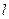 的方程
的方程