(本小题满分16分)已知椭圆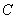 :
: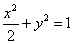 的左、右焦点分别为
的左、右焦点分别为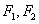 ,下顶点为
,下顶点为 ,点
,点 是椭圆上任一点,⊙
是椭圆上任一点,⊙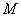 是以
是以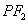 为直径的圆.
为直径的圆.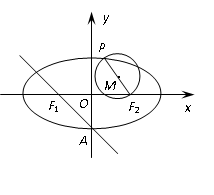
(Ⅰ)当⊙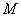 的面积为
的面积为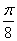 时,求
时,求 所在直线的方程;
所在直线的方程;
(Ⅱ)当⊙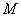 与直线
与直线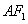 相切时,求⊙
相切时,求⊙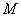 的方程;
的方程;
(Ⅲ)求证:⊙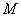 总与某个定圆相切.
总与某个定圆相切.
推荐套卷
(本小题满分16分)已知椭圆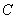 :
: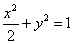 的左、右焦点分别为
的左、右焦点分别为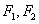 ,下顶点为
,下顶点为 ,点
,点 是椭圆上任一点,⊙
是椭圆上任一点,⊙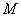 是以
是以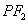 为直径的圆.
为直径的圆.
(Ⅰ)当⊙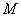 的面积为
的面积为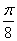 时,求
时,求 所在直线的方程;
所在直线的方程;
(Ⅱ)当⊙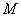 与直线
与直线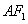 相切时,求⊙
相切时,求⊙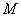 的方程;
的方程;
(Ⅲ)求证:⊙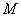 总与某个定圆相切.
总与某个定圆相切.