(本小题满分16分)
某广告公司为2010年上海世博会设计了一种霓虹灯,样式如图中实线部分所示. 其上部分是以 为直径的半圆,点
为直径的半圆,点 为圆心,下部分是以
为圆心,下部分是以 为斜边的等腰直角三角形,
为斜边的等腰直角三角形, 是两根支杆,其中
是两根支杆,其中 米,
米, . 现在弧
. 现在弧 、线段
、线段 与线段
与线段 上装彩灯,在弧
上装彩灯,在弧 、弧
、弧 、线段
、线段 与线段
与线段 上装节能灯. 若每种灯的“心悦效果”均与相应的线段或弧的长度成正比,且彩灯的比例系数为
上装节能灯. 若每种灯的“心悦效果”均与相应的线段或弧的长度成正比,且彩灯的比例系数为 ,节能灯的比例系数为
,节能灯的比例系数为 ,假定该霓虹灯整体的“心悦效果”
,假定该霓虹灯整体的“心悦效果” 是所有灯“心悦效果”的和.
是所有灯“心悦效果”的和.
(Ⅰ)试将 表示为
表示为 的函数;
的函数;
(Ⅱ)试确定当 取何值时,该霓虹灯整体的“心悦效果”最佳?
取何值时,该霓虹灯整体的“心悦效果”最佳?
推荐套卷
 ,直线/的方程为
,直线/的方程为
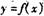
 .的切线,求证I
.的切线,求证I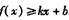 对任意
对任意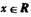 成立;
成立; 对任意
对任意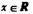 成立,求实数k,b应满足的条件.
成立,求实数k,b应满足的条件. 点C
点C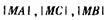 成等比数列;
成等比数列;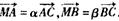 ,试问,
,试问,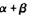 是否为定值,若是,求出此定值;若不是,请说明理由.
是否为定值,若是,求出此定值;若不是,请说明理由.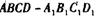 中,DA = DC
中,DA = DC =2,
=2,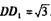 ’E是
’E是 的中点,F是C/:的中点.
的中点,F是C/:的中点.
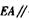 平面BDF
平面BDF 平面
平面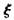 表示将两件不合格产品全部检测出来后四件合格产品中报废品的数量.
表示将两件不合格产品全部检测出来后四件合格产品中报废品的数量. 满足
满足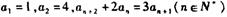 .
. 的通项公式
的通项公式
 的前n项和
的前n项和 .求使得
.求使得 成立的最小整数n
成立的最小整数n 粤公网安备 44130202000953号
粤公网安备 44130202000953号