如图，DC⊥平面ABC，EB//DC，AC=BC=EB=2DC=2，∠ACB=120°，P，Q分别为AE、AB的中点。
（I）证明：PQ//平面ACD；
（II）求异面直线AE与BC所成角的余弦值；
（III）求平面ACD与平面ABE所成锐二面角的大小。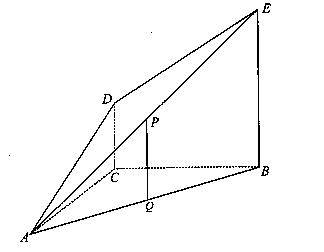
相关试题
，
的值；
，求边AC的长。
的表达式，并求函数
，是否存在实数m，使函数
的值域恰为
？若存在，请求出m的取值；若不存在，请说明理由。
，
（I）求A的大小；（II）求
的值.
．
，求
的最大值和最小值；
，求
的值．
，且
与
是方程
的两个根.
的值;
，求BC的长.推荐套卷
如图，DC⊥平面ABC，EB//DC，AC=BC=EB=2DC=2，∠ACB=120°，P，Q分别为AE、AB的中点。
（I）证明：PQ//平面ACD；
（II）求异面直线AE与BC所成角的余弦值；
（III）求平面ACD与平面ABE所成锐二面角的大小。
粤公网安备 44130202000953号