为加强环保建设,提高社会效益和经济效益,某市计划用若干年时间更换一万辆燃油型公交车,每更换一辆新车,则淘汰一辆旧车,替换车为电力型和混合动力型车,今年初投入了电力型公交车128辆,混合动力型公交车400辆;计划以后电力型车每年的投入量比上一年增加50%,混合动车型车每年比上一年多投入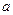 辆。
辆。
(1)求经过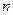 年,该市被更换的公交车总数
年,该市被更换的公交车总数 ;
;
(2)若该市计划7年内完成全部更换,求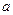 的最小值。
的最小值。
推荐套卷
为加强环保建设,提高社会效益和经济效益,某市计划用若干年时间更换一万辆燃油型公交车,每更换一辆新车,则淘汰一辆旧车,替换车为电力型和混合动力型车,今年初投入了电力型公交车128辆,混合动力型公交车400辆;计划以后电力型车每年的投入量比上一年增加50%,混合动车型车每年比上一年多投入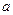 辆。
辆。
(1)求经过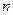 年,该市被更换的公交车总数
年,该市被更换的公交车总数 ;
;
(2)若该市计划7年内完成全部更换,求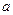 的最小值。
的最小值。