（请考生在题22，23，24中任选一题作答，如果多做，则按所做的第一题计分。）
（本小题满分10分）如图5，⊙O1和⊙O2公切线AD和BC相交于点D，A、B、C为切点，直线DO1与⊙O1与E、G两点，直线DO2交⊙O2与F、H两点。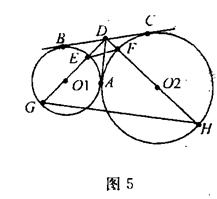
（1）求证：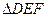
～
；
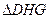（2）若⊙O1和⊙O2的半径之比为9：16，求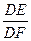
的值。
相关试题
平面
，四边形ABCD为直角梯形，
//
，
，
，,
．
//平面
；
平面
；
的余弦值．
与
轴的正半轴的交点为
，点
、
在圆
，
．
，求
的值．
中，内角
的对边分别是
，已知
，且
，求边长
中，底面
是矩形，
是
的中点，
是
的中点。
与
所成的角；（Ⅱ）求二面角
的大小。
，各局比赛结果相互独立。
，求推荐套卷
（请考生在题22，23，24中任选一题作答，如果多做，则按所做的第一题计分。）
（本小题满分10分）如图5，⊙O1和⊙O2公切线AD和BC相交于点D，A、B、C为切点，直线DO1与⊙O1与E、G两点，直线DO2交⊙O2与F、H两点。
（1）求证：～；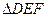
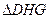（2）若⊙O1和⊙O2的半径之比为9：16，求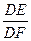的值。
粤公网安备 44130202000953号