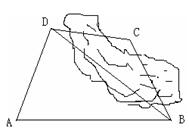
如图，为了计算某湖岸边两景点B与C的距离，由于地形的限制，需要在岸上A和D两个测量点，现测得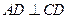
，AD="10km,AB=14km," 
, 
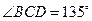，求两景点B与C之间的距离（假设A、B、C、D在同一平面内，测量结果精确到0.1km,参考数据：
）
，
，求
及
、
间的夹角
（精确到
）．
中，
，
，你能用
，
表示向量
，
吗？
外的一点，过P作圆的切线，试求过两切点的切点弦所在的直线方程。
轴上，且过点A（1，4），B（2，
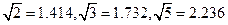）的圆的方程。相关知识点
推荐套卷
如图，为了计算某湖岸边两景点B与C的距离，由于地形的限制，需要在岸上A和D两个测量点，现测得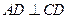，AD="10km,AB=14km," , 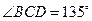，求两景点B与C之间的距离（假设A、B、C、D在同一平面内，测量结果精确到0.1km,参考数据： ）
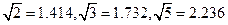粤公网安备 44130202000953号