(本小题满分12分)
如图，在四棱锥P—ABCD中，底面ABCD是矩形，已知AB = 3，AD = 2，PA = 2，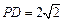
，
．
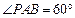(1) 证明：AD⊥平面PAB；
(2) 求异面直线PC与AD所成的角的大小；
(3) 求二面角P—BD—A的大小．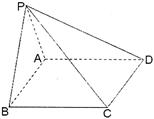
相关试题
.
，求△ABC的周长L的取值范围.
，使得
的最大值为
，若存在，求出
,
在一个周期内，当
时，
取得最小值
；当
时，
，再将图像沿
轴向右平移
个单位，得到函数
的图像.
.
上的值域.推荐套卷
(本小题满分12分)
如图，在四棱锥P—ABCD中，底面ABCD是矩形，已知AB = 3，AD = 2，PA = 2，，．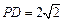
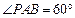(1) 证明：AD⊥平面PAB；
(2) 求异面直线PC与AD所成的角的大小；
(3) 求二面角P—BD—A的大小．
粤公网安备 44130202000953号