(本小题满分12分)已知向量 ,
, .
.
(1)若 ,
, 分别表示将一枚质地均匀的正方体骰子(六个面
分别表示将一枚质地均匀的正方体骰子(六个面 的点数分别为1,2,3,4,5,6)先后抛掷两次时第一次、第二次出现的点数,求满足
的点数分别为1,2,3,4,5,6)先后抛掷两次时第一次、第二次出现的点数,求满足 的
的 概率;
概率;
(2)若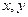
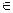
 ,求满足
,求满足 的概率.
的概率.
推荐套卷
(本小题满分12分)已知向量 ,
, .
.
(1)若 ,
, 分别表示将一枚质地均匀的正方体骰子(六个面
分别表示将一枚质地均匀的正方体骰子(六个面 的点数分别为1,2,3,4,5,6)先后抛掷两次时第一次、第二次出现的点数,求满足
的点数分别为1,2,3,4,5,6)先后抛掷两次时第一次、第二次出现的点数,求满足 的
的 概率;
概率;
(2)若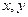
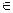
 ,求满足
,求满足 的概率.
的概率.