(本小题满分12分)
用黄、蓝、白三种颜色粉刷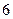
间办公室
(Ⅰ)若每间办公室刷什么颜色不要求，有多少种不同的粉刷方法？
(Ⅱ)若一种颜色粉刷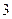
间，一种颜色粉刷
间，一种颜色粉刷
间，有多少种不同的粉刷方法？
（Ⅲ）若每种颜色至少用一次，粉刷这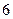间办公室，有多少种不同的粉刷方法？
的球内作一内接圆柱，这个圆柱的底面半径和高为何值时，它的侧面积最大？并求此最大值.
求实数
的值；
，
.求实数
，且
求证：
，（
）其定义域为
（
）,设
.（1）试确定
的取值范围,使得函数
在
的大小并说明理由．推荐套卷
(本小题满分12分)
用黄、蓝、白三种颜色粉刷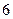间办公室
(Ⅰ)若每间办公室刷什么颜色不要求，有多少种不同的粉刷方法？
(Ⅱ)若一种颜色粉刷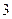间，一种颜色粉刷间，一种颜色粉刷间，有多少种不同的粉刷方法？
（Ⅲ）若每种颜色至少用一次，粉刷这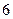间办公室，有多少种不同的粉刷方法？
粤公网安备 44130202000953号