(本小题满分13分)
给定椭圆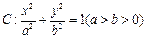 ,称圆心在原点
,称圆心在原点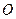 ,半径为
,半径为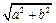 的圆是椭圆C的“准圆”.若椭圆C的一个焦点为
的圆是椭圆C的“准圆”.若椭圆C的一个焦点为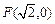 ,其短轴上的一个端点到F的距离为
,其短轴上的一个端点到F的距离为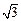 .
.
(I)求椭圆C的方程和其“准圆”方程;
(II )点P是椭圆C的“准圆”上的一个动点,过点P作直线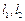 ,使得
,使得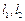 与椭圆C都只有一个交点,且
与椭圆C都只有一个交点,且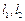 分别交其“准圆”于点M,N .
分别交其“准圆”于点M,N .
(1)当P为“准圆”与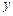 轴正半轴的交点时,求
轴正半轴的交点时,求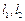 的方程;
的方程;
(2)求证:|MN|为定值.
推荐套卷
(本小题满分13分)
给定椭圆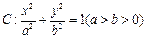 ,称圆心在原点
,称圆心在原点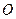 ,半径为
,半径为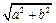 的圆是椭圆C的“准圆”.若椭圆C的一个焦点为
的圆是椭圆C的“准圆”.若椭圆C的一个焦点为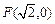 ,其短轴上的一个端点到F的距离为
,其短轴上的一个端点到F的距离为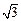 .
.
(I)求椭圆C的方程和其“准圆”方程;
(II )点P是椭圆C的“准圆”上的一个动点,过点P作直线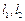 ,使得
,使得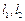 与椭圆C都只有一个交点,且
与椭圆C都只有一个交点,且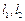 分别交其“准圆”于点M,N .
分别交其“准圆”于点M,N .
(1)当P为“准圆”与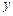 轴正半轴的交点时,求
轴正半轴的交点时,求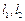 的方程;
的方程;
(2)求证:|MN|为定值.